由低估换更低估产生的思考——论投资方式 、 持股周期以及盈利数学期望间的关系

一 、 思考由来

昨日在我的投资底稿中偶然发现了2016年11月14日的港股通持仓细节如下 ， 并且突发奇想的测算了一下假设这些持仓不动的持有至今的结果如下：



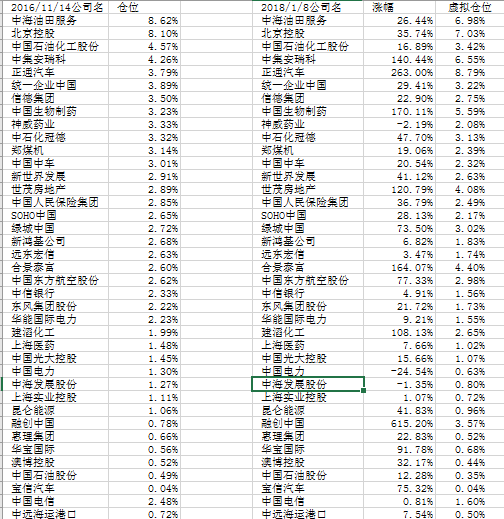
若持仓不动 ， 这14个月不到的时间的收益情况在考虑汇率变化后按照人民币计价如下：



而事实上 ， 我的投资模型中有一条就是“低估换更低估” ， 即若个人判断有更低估的股票 ， 可以将持仓中相对稍贵的低估股票卖出 ， 并换入更低估股票 。 就是这一点 ， 导致我同期的真实持仓净值按照人民币计价仅上涨22% ， 落后了25个百分点！ 才一年多的时间损失巨大 。 因此我对此做了深入的思考 ， 由此得到本篇心得并随之修改我的投资体系 。

二 、 一些定义

本文主要讨论投资方式 、 持股周期以及盈利数学期望之前的关系 ， 我们需要熟悉一下名词定义 ， 在下文中会大量用到 ， 我就不会再一一解释了 。

持股周期T： 一只股票从买入到卖出的时长

投资方式： 1. 价值投资： 仅指格雷厄姆式价值投资 ， 也即只使用安全边际 ， 不使用护城河分析的价值投资 。 关于这两者的详细辨析 ， 若有兴趣请参考我以前的文章 ， 在此不再解释： http://www.myzaker.com/article/594d02ddd1f149d35c00006f/

2. 趋势投资： 定义为追涨杀跌配以大量止损的动量方法

盈利的数学期望：

1.概率P： 基于当下时点的赚钱概率

2.赔率b： 基于当下时点的盈利幅度

3.数学期望E=概率P*赔率b： 基于当下时点的盈利期望

为了深入分析这些因素的关系 ， 我们需要采用物理学中的控制变量法去控制一些其他可控变量 ， 以下为这些变量的定义以及控制方法：

1. 企业的竞争优势 （护城河） ： 我们假设我们选择的公司只使用了安全边际 ， 而没有分析其竞争优势 。 熟悉我的朋友应该知道我使用安全边际 （即低估） 时必须结合“分散” ， 即持有一篮子不同行业不同市场甚至不同国家的低估公司来进行风险的分散 。 分散是对无法认知企业竞争优势的妥协 ， 所以这是我控制的第一个变量 ， 也即假设在分散的情况下 ， 我持有的一篮子股票的竞争优势和市场本身保持一致 ， 有些有护城河 ， 有些没护城河 ， 有些慢慢变坏 ， 但综合来看保持平均水平 。
2. 仓位： 基于分散的前提 ， 对于仓位 ， 我们采取平均分配的方法 ， 也即无法认知组合中的股票孰优孰劣的情况下使用的方法 。
3. 情绪： 情绪成本为0 ， 即不存在一时脑热突破投资模式 ， 也不存在一时冲动后运气好取得超额收益的情况

控制上述变量后 ， 我们的分析对象可以简化为一个组合 。 该组合是基于安全边际的原则构建的 ， 组合内部采取平均分配持仓 ， 且个股的定性护城河水准和指数整体保持一致 。

在正式分析前 ， 我们还需要明确一点 ， 该组合在动态换仓情况下可以长期取得超过指数平均水平的盈利数学期望 。 动态换仓是指机械的将组合中在历史估值中位值以上的个股卖出 ， 重新买入其他的低估股票 ， 不断轮动 。 对这一点有疑问的 ， 我建议也可以看下前几段给的那个链接中的文章 ， 相信会对安全边际有更深的把握 ， 在此也不赘述了 。

三 、 盈利数学期望E 、 持股周期T和投资方式的关系

T和投资方式的关系： 持股周期越长 ， 股价受基本面的驱动越大 ， 按年为周期后 ， 基本不受到市场资金和情绪的影响 ， 价值投资越有效； 反之持股时间越短 ， 趋势投资越有效 。

在上述前提下 ， 我们再将盈利数学期望E放入思考模型 ， 为了和持股时间T相匹配：

1. 在小周期下的趋势投资必然是低概率的 ， 因此要取得超越市场的盈利数学期望E （超额数学期望 ， 下同） ， 必须是高赔率的 ， 而高赔率的实现又需要拉长盈利股票的持股周期 ， 而对于亏损股票则采取灵敏的止损点 。 简而言之 ， 一个长期成功的趋势投资者 （此处不讨论投资和投机的差异问题 ， 完全是策略和持股周期的不同而已） ， 应该是具有分散持仓 、 止损点灵敏和让盈利奔跑的特点 。 和上述特点不符的 ， 没有超额数学期望 ， 及时短暂成功也是幸存者偏差 ， 不能算成功的趋势投资者 。
2. 在长周期下 ， 价值投资应具有中级别概率 ， 同时中概率本身却神奇的配合了高赔率 （越深的安全边际同时配合了越高的盈利值和概率） 。 为何价值投资具有中概率的特点 ， 这主要是因为受到参与者羊群效应的影响 ， 市场会高估企业的恶劣程度 ， 从而带来概率优势 。 而是中概率 ， 不是高概率是因为： 概率本身除了受到市场悲观情绪带给价值投资者的正面影响外 ， 还受到企业本身的影响 ， 企业持续恶化直至破产的可能性是存在的 ， 因此我人为定义为中概率 。

所以趋势投资者的优势在于其止损后的资金可以很快投入下一场战役 ， 缩短了整个组合的持股周期 ， 提高了资金使用效率 ， 对于明白需要配合高赔率的趋势投资者而言 ， 其盈利来自于收割其他不明白“让利润奔跑”和“分散降低低概率劣势”的参与者的智商税 。

而价值投资的优势在于其中等概率的盈利可能 ， 以及安全边际带来的高赔率优势 ， 两者结合可以产生更为有利的盈利数学期望 。 但其持股周期相对趋势投资要长 。

两者对比 ， 由于交易费用的存在 ， 价值投资者更有优势 。 当然 ， 这结论是基于上文所定义的正确的价值投资和趋势投资的模型 ， 至于赔率 、 概率 、 持股周期的综合安排出现错误的投资方式 ， 不在讨论范围内 。

因此 ， 我去年投资的愚蠢是在于没有将高赔率的特点理解明晰 ， 而采用了“低估换更低估”的方式来降低了自己的持股周期 。 回头看施洛斯的描述就如醍醐灌顶：

“他也不换股 。 从理论上说 ， 这么做是最聪明的 ， 发现有更便宜的股票时 ， 卖出A买入B 。 从逻辑上讲 ， 要是有更便宜的股票 ， 应该换股 。 要判断不同行业的公司的相对价值非常难 ， 很难得出一个具体的数字来 。 另外 ， 他买的很多股票都要几年时间才能达到预期 ， 不是一买就涨 。 一只股票一步步渐入佳境 ， 你也慢慢熟悉这只股票 。 要是因为相对价值换股 ， 在新买入的股票上再熬三年 ， 这些东西都有个生命周期 。 所以 ， 他不愿意用A换B 。”

请注意生命周期的概念 ， 这就是本文所说的持股周期 。 如果本文到此结束 ， 无非是重复了一遍施洛斯伟光正的投资理念 。 “低估换更低估”从逻辑上无疑是正确的 ， 因为价值投资本就基于安全边际 ， 而你无法拒绝一只更有安全边际的股票 ， 这是价值投资的核心 。 但是一句轻飘飘的“判断相对价值非常难”并不足以将之作为动摇我们核心宗旨的稻草 。 就如同你的宗旨如果是以阶级斗争为纲但却行以经济发展为中心的政治 ， 则名不正言不顺 ， 必须也将宗旨改为以经济发展为中心才可以 。 而我们的宗旨为安全边际 ， 但实际上却并不以此为标准 ， 则是非难分 。

为想通这一问题 ， 我们需要运用芒格的栅格思维去在高纬度去思考这一问题 。 这就如同政府的宗旨确实是为人民谋利 ， 但是有时为了满足总体人民利益最大化的原则 ， 可能牺牲了部分人民的利益 ， 比如某些低薪但工作繁重的职业 ， 某些工业化初期必须得到的廉价劳动力资源等等 ， 有了这些牺牲 ， 形成了一个高度工业化和现代化的社会 ， 则总体共赢 。 又如军费如果投入民生 ， 短期民众确实得利了 ， 但国防不强若被敌侵略 ， 则皮之不存毛将焉附 ， 长期人民整体利益的数学期望是负值 。 我们试着从这一角度去想 。

以下所以假设都基于个股风险通过分散解决 ， 而内在价值判断的误差也通过分散解决的控制变量法之前提下进行 。

四 、 多角度思考

1 数学归纳法

我们可以使用数学归纳法来证伪“低估换更低估”这一理论 。 举个例子 ， 一只内在价值1元的股票 ， 买入时0.5元 ， 某日涨到了0.6元 ， 同时 ， 投资者又发现了另一只内在价值1元而市场价格0.5元的股票 ， 于是他实行了“低估换更低估”的策略换股 。

我们假设 ， 该投资者只是恰巧在这天复盘了 ， 而事实上我们要去想为何他不在0.55元换股？ 0.51元呢？ 0.500001元呢 （忽视交易费用） ？ 运用数学归纳法来无限微分下去这一场景 ， 我们会发现我们陷入了一种悖论 ， 即相对价值差异阈值和现实环境的悖论 。 这种悖论的存在是由于忽视了上文所说的持股周期T 。 价值投资必须要和中长期的持股周期做匹配 ， 否则看似在用“低估换更低估”来践行安全边际的宗旨 ， 但实际上却在行使错误的持股周期 。 就如同一个为民谋利为宗旨的政府 ， 为了短期民意 ， 却损失了长期的民众利益 （希拉里？ 大麻合法化？ 哈哈） 。

2 生物学

生物学还是主要是从羊群效应去思考这一问题 。 羊群效应从发酵到高潮 ， 其传播速率是加速度的 ， 因此在一个向上的羊群效应周期里 ， 其赔率的斜率是逐渐提高的 。 从1元到10元 ， 可能花了2年 ， 从10元到100元 ， 可能只需要1年 。 前者赚了9元 ， 花了2年； 后者赚了90元 ， 才花了1年 。 这更像施洛斯所说的生命周期 ， 其实是羊群效应的周期 （当然可能结合基本面反转） 。 我一直觉得索罗斯是个天才 ， 尽管他不是价值投资者 ， 但他的名言： ”世界经济史是一部基于假象和谎言的连续剧 。 要获得财富做法就是认清其假象投入其中然后在假象被公众认识之前退出游戏 。 ”似乎和施洛斯的说法殊途同归了 。 假设一个市场预期从0到100的羊群效应扩散周期 ， 施洛斯基于安全边际的原则 ， 可能在预期为10的时候买入 ， 在70的时候退出了 。 而索罗斯可能在预期50的时候才进入 ， 在预期为80的时候退出了 。 由于赔率的斜率是提高的 ， 所以预期10-70相比预期50-80而言 ， 后者索罗斯的模式赚的可能比前者还多一点 ， 时间也更短一点 （传播速率后期加速） ， 但是索罗斯模式的概率是较低的 ， 而施洛斯的成功概率是相对较高的 。

3 社会学

主要是二八原则的讨论 ， 尽管帕累托定律最初是个数学概念 ， 但最常使用的还是社会学中 。

假设在理想的无阻力环境下 （1.无交易费用； 2.参与者100%理性） ， 将盈利的数学期望微分化会发现其斜率始终一样 ， 也就是说不存在超额的数学期望 。 但事实上 ， 由于人的差异在市场参与者中自然形成了二八现象 ， 比如20%的人盈利 ， 80%的人亏损 。 所以 ， 在某些奇点 ， 一定会产生斜率变化 ， 从而产生超额收益 。 只针对持股周期而言 ， 也即一定存在某个最优持股周期 ， 在该周期到的时候卖出 ， 其盈利的数学期望是最优化的 。 由前文得知 ， 这一周期在价值投资框架下一定不是短期的 ， 而是长期的 ， 问题只是我们不知道究竟是一年 、 两年 、 还是四年 ， 施洛斯认为是4年 。 而且 ， 这个最优持股周期针对具体股票也是不一样的 ， 但我们依然可以用分散的方法来控制这一变量 。

那么最优持股周期由哪些因素决定呢 ， 我想可能是以下因素：

(1)羊群效应的强弱： 受到通讯速度 、 羊群基数 、 参与者教育程度和社会习俗等的影响 。

(2)经济与行业周期： 经济或行业周期的长短的现实因素

(3)人的生命长度

4 物理学

想到这里 ， 我曾经花了很长时间思考最优持股周期 ， 但是在使用物理学模型嵌套的时候 ， 我就觉得我可能走入歧途了 ， 因为又使用了经典物理学的线性逻辑推理来顺藤摸瓜去摸索超额数学期望奇点的特征 ， 而这是行不通的 ， 尽管我个人为满足模型的对称性将这奇点设置在预期20%-80%之间 ， 以符合二八原则的完美 ， 潜台词就是在预期0%-20%之间 ， 可能会导致过高的误判成本 ， 从而导致“在等底部 ， 然后股价开始长周期上涨错失买入机会”的现象过多 ， 而在80%-100%之间 ， 则存在概率减小的突变点 ， 从而导致数学期望的损失 。

当然 ， 这个值是不存在定值的 ， 上面我只是举个例子 ， 但我现在认为这个点一定高于50% 。

放弃线性逻辑 ， 对于微观世界的电子轨道既然可以使用量子力学来给出不确定的结果 ， 那么对于最优持股周期可以同样如此 。 微观的不确定性导致了宏观上的确定性 ， 也即存在一个理论可以模糊的统一持股周期和数学期望的关系 。 如果不断的尝试 ， 不断的对事后的结果进行最优持股周期的回顾 ， 应该会发现其结果会聚集与某个奇点附近 ， 而这个点虽然不确定 ， 但我们知道会在高于50%的某个点 ， 这也就和“低估换更低估”的理念产生了冲突 ， 从而间接倾斜了“低估换更低估”的机械安全边际方法的基石 。

5 反身性和预期差

反身性原理大家应该很熟悉了 ， 不再做介绍了 ， 我先借索罗斯的一张图：



高点的差异主要是由于羊群效应引起的群体过于乐观从而造成负预期差 （现实-预期） 而造成 ， 同样的 ， 在低估领域 ， 同样存在某股价最低点 ， 该最低点领先于市场的悲观预期最低点 ， 从而形成正预期差 。 价值投资就是在有正预期差的时刻购入 ， 这一点是安全边际的意义 。

而卖出 ， 结合前文所述 ， 我个人也认为需要在负预期差的时刻卖出 。 而负预期差也只有在超过50%的羊群预期后才会出现 （即乐观情绪） ， 我个人希望把这个奇点理解为80% ， 无论如何 ， 在低估阶段就亟不可待的换更低估 ， 也不符合上述模型假设 。

五 、 总结

差不多想到这里 。 我将个人投资模型做了调整 。 在低估和分散的核心外 ， 对个股不再进行“低估换更低估”的操作 ， 只进行“高估换低估”操作 。 过快换股意味着和价值投资的持股周期产生冲突 ， 并且也没有充分利用羊群效应 ， 而且从高阶来看 ， 和二八模型和反身性原理也有自相矛盾之处 。 多角度来看 ， 低估换更低估的做法尽管在逻辑上完全符合安全边际原则 ， 但将其放在更宏观的角度来看存在问题 。 再举几个不恰当的例子：

1 我认为差异性是一个优良的社会系统的基本特点 ， 对于价值观高度雷同或两分的社会 ， 该复杂系统的稳定性反而不如多样化系统 。 多样化系统中的分子随机运行 ， 看似混乱却恰恰可以兼容并蓄 、 稳定发展； 相信我们对比下改革开发前后就会有所体会 。 同样的 ， 过于执着于窄幅安全边际 ， 而忽略了如持股周期等其他因素 ， 恰恰类似于单一价值观社会 ， 激昂但并不合理 。

2 同样的 ， 一个明智的学生 ， 应该将时间合理安排在不同科目上 ， 尽量不偏科 ， 毕竟从0分提高到60分比从90提高到100分容易多了 ， 其数学期望是严重不对称的 。 因此 ， 过于执着于在安全边际上从90分做到100分 ， 也许并不成功 ， 反而丧失了其他的有利因素 。

3 结合中庸的观点来看 ， 充满想象力的人是好的 ， 而充满幻想的人则不一定好了 ， 而幻想和想象之间从无清晰的界限 ， 你无法想象存在某条线 ， 在79.99分时是全世界最有想象力的人 ， 而在80分时就变成个幻想症患者 。 所以 ， 受到合理限制是一种福气 ， 家里有管你的老婆看似不好 ， 但实际上对你的人生是有益的； 使用安全边际是最重要的 ， 但是不能走向毫无限制的极端 ， 从而导致改变了复杂系统的其他因子规则 ， 反而损失了数学期望 。

啰啰嗦嗦一大堆 ， 到最后还是施洛斯的那段话：

“这些东西都有生命周期 ， 我们大约每4年换一次股”

“这些东西都有生命周期 ， 我们大约每4年换一次股”

“这些东西都有生命周期 ， 我们大约每4年换一次股”

大道至简 ， 对于格雷厄姆和施洛斯等大师只能再次献上一个小学生卑微的膝盖 。